Funções de Probabilidade

Definição

  • Funções de probabilidade são funções matemáticas que descrevem a distribuição de probabilidade de uma variável aleatória.
  • Elas atribuem uma probabilidade a cada possível resultado dessa variável aleatória.
  • Existem diferentes tipos de funções de probabilidade, dependendo do tipo de variável aleatória em questão.
  • Função de probabilidade discreta: Usada quando a variável aleatória é discreta, ou seja, pode assumir valores contáveis. Exemplos: Bernoulli, Binomial, Poisson
  • Função de densidade de probabilidade (PDF): Usada quando a variável aleatória é contínua, ou seja, pode assumir qualquer valor dentro de um intervalo. Exemplos: Normal (Guassiana), Exponencial e Uniforme
  • Essas funções são fundamentais em estatística e teoria das probabilidades para entender e modelar o comportamento de variáveis aleatórias em diferentes contextos.

Em R

  • Para cada distribuição de probabilidade existem quatro funções no R. Cada uma delas é chamada adicionando o seguinte prefixo ao nome da distribuição correspondente:

    • - d - para a função de massa ou densidade.

    • - p - para a função de distribuição (cumulativa).

    • - q - para quantis, ou seja, para calcular o valor correspondente para a função de distribuição cumulativa dada uma probabilidade.

    • - r-para gerar amostras aleatórias com a distribuição dada.

Discrete Distribution Name Continuous Distribution Name
Binomial (binom) Normal (norm)
Negative binomial (nbinom) Exponential (exp)
Geometric (geom) Uniform (unif)
Poisson (pois) Gama (gamma)

Distribuição Binomial

  • A distribuição binomial é usada para modelar o número de sucessos (xx) em um número fixo de tentativas (nn) independentes, onde cada tentativa tem a mesma probabilidade (pp) de sucesso.

P(X=x)=(nx)px(1−p)n−x P(X = x) = \binom{n}{x} p^x (1-p)^{n-x}

  • Suponha que estamos lançando uma moeda justa 10 vezes e queremos calcular a probabilidade de obter exatamente 4 caras.
# Função dbinom() para calcular a probabilidade em uma distribuição binomial
probabilidade <- dbinom(x=4, size = 10, prob = 0.5)
print(probabilidade)
[1] 0.2050781
  • Suponha que estamos lançando uma moeda justa 10 vezes e queremos calcular a probabilidade de obter no máximo 4 caras.
probabilidade <- pbinom(q=4, size = 10, prob = 0.5)
print(probabilidade)
[1] 0.3769531
  • Simulando valores
N = 20
n = 1
(x = rbinom(N,n,prob = 0.5))
 [1] 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 0
(table(x))
x
 0  1 
 4 16

Distribuição de Poisson

  • A distribuição de Poisson modela a probabilidade de um número de eventos (xx) ocorrer em um intervalo fixo de tempo ou espaço, dado um número médio (λ\lambda) de eventos que ocorrem nesse intervalo.

P(X=x)=e−λλxx! P(X = x) = \frac{e^{-\lambda} \lambda^x}{x!}

  • Suponha que em média 2 clientes entram em uma loja por minuto. Queremos calcular a probabilidade de exatamente 3 clientes entrarem na loja em um minuto específico.
# Função dpois() para calcular a probabilidade em uma distribuição de Poisson
probabilidade <- dpois(3, lambda = 2)
print(probabilidade)
[1] 0.180447
  • Suponha que em média 2 clientes entram em uma loja por minuto. Queremos calcular a probabilidade de até 3 clientes entrarem na loja em um minuto específico.
probabilidade <- ppois(3, lambda = 2)
print(probabilidade)
[1] 0.8571235
  • Simulando valores
x <- rpois(n = 10, lambda = 2)
table(x)
x
0 1 2 4 6 
2 2 4 1 1

Distribuição Normal

  • A distribuição normal (gaussiana) é usada para modelar uma grande variedade de fenômenos com variáveis contínuas. É caracterizada por sua forma de sino e é completamente determinada por sua média e desvio padrão.

f(x)=1σ2πe−12(x−μσ)2 f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} \left(\frac{x - \mu}{\sigma}\right)^2}

  • xx é a variável aleatória,

  • μ\mu é a média da distribuição,

  • σ\sigma é o desvio padrão da distribuição.

  • Suponha que estamos analisando os resultados de um teste padronizado em que a pontuação média é 100 e o desvio padrão é 15. Queremos calcular a probabilidade de um aluno ter uma pontuação abaixo de 110.

# Função pnorm() para calcular a probabilidade em uma distribuição normal
probabilidade <- pnorm(110, mean = 100, sd = 15)
print(probabilidade)
[1] 0.7475075
  • Suponha que estamos analisando os resultados de um teste padronizado em que a pontuação média é 100 e o desvio padrão é 15. Queremos calcular a probabilidade de um aluno ter uma pontuação entre 110 e 120.
probabilidade <- pnorm(120, mean = 100, sd = 15) - pnorm(110, mean = 100, sd = 15)
print(probabilidade)
[1] 0.1612813
  • Suponha que estamos analisando os resultados de um teste padronizado em que a pontuação média é 100 e o desvio padrão é 15. Queremos calcular a probabilidade de um aluno ter uma pontuação maior que 120.
probabilidade <- pnorm(120, mean = 100, sd = 15,lower.tail = F) 
print(probabilidade) # ou
[1] 0.09121122
probabilidade <- 1-pnorm(120, mean = 100, sd = 15,lower.tail = T) 
print(probabilidade)
[1] 0.09121122
  • Quantis
qnorm(0.75,mean = 100,15)
[1] 110.1173
qnorm(0.09,mean = 100,15,lower.tail = F)
[1] 120.1113
  • Simulando valores
z = rnorm(1000,mean = 0,sd = 1)
x1 = rnorm(10000,mean = 100,sd = 1)
x2 = rnorm(1000,mean = 100,sd = 10)
x3 = rnorm(1000,mean = 10,sd = 10)
par(mfrow=c(2,2))
hist(z);hist(x1);hist(x2);hist(x3)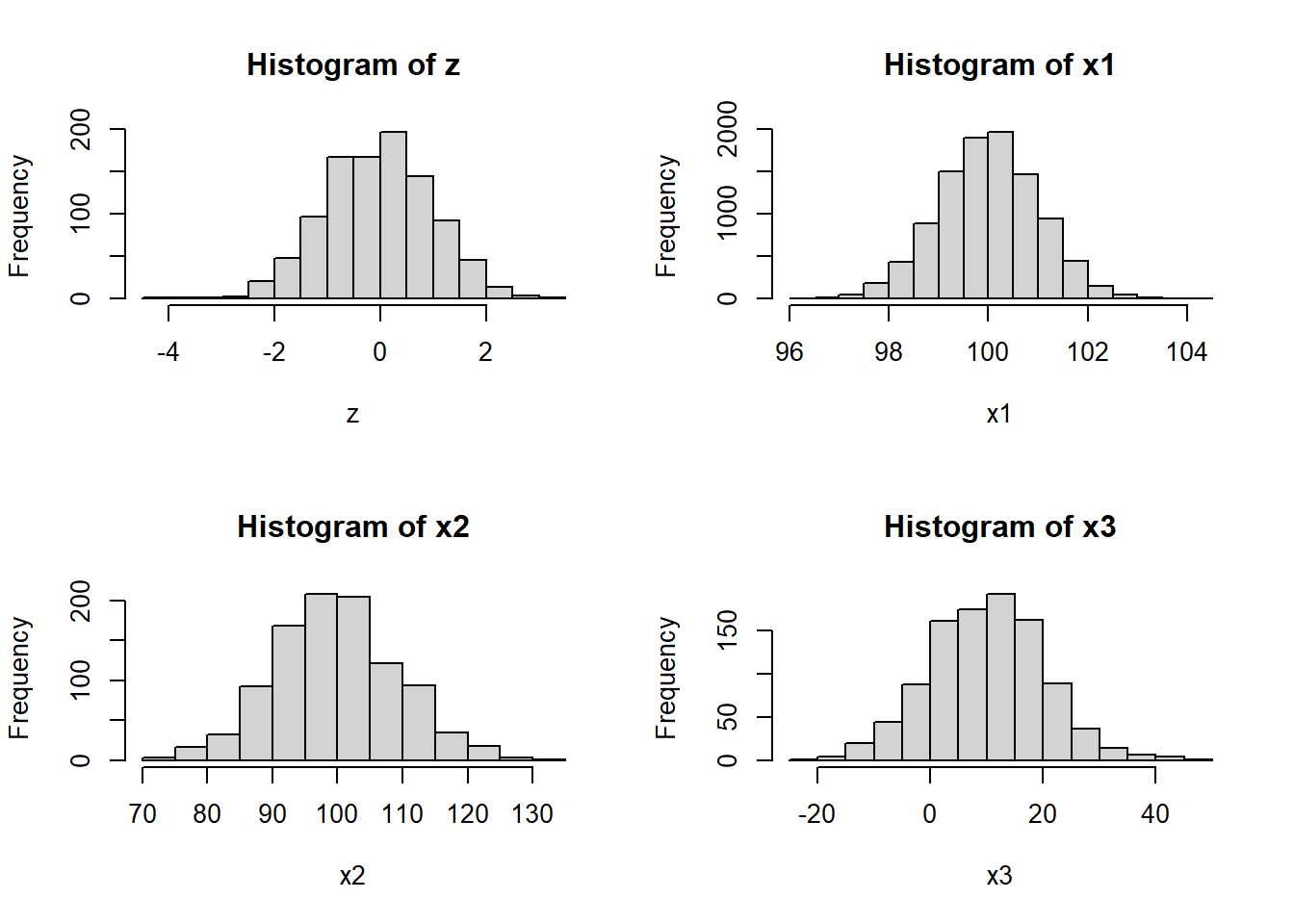

  • f(x)f(x)
# Parâmetros da distribuição normal
mu <- 0  # Média
sigma <- 1  # Desvio padrão

# Valores para o eixo x
x <- seq(-4, 4, length.out = 100)

# Calculando os valores da densidade de probabilidade para os valores de x
y <- dnorm(x, mean = mu, sd = sigma)

# Plotando a curva da distribuição normal
plot(x, y, type = "l", lwd = 2, col = "blue", 
     main = "Curva da Distribuição Normal", 
     xlab = "x", ylab = "Densidade de Probabilidade")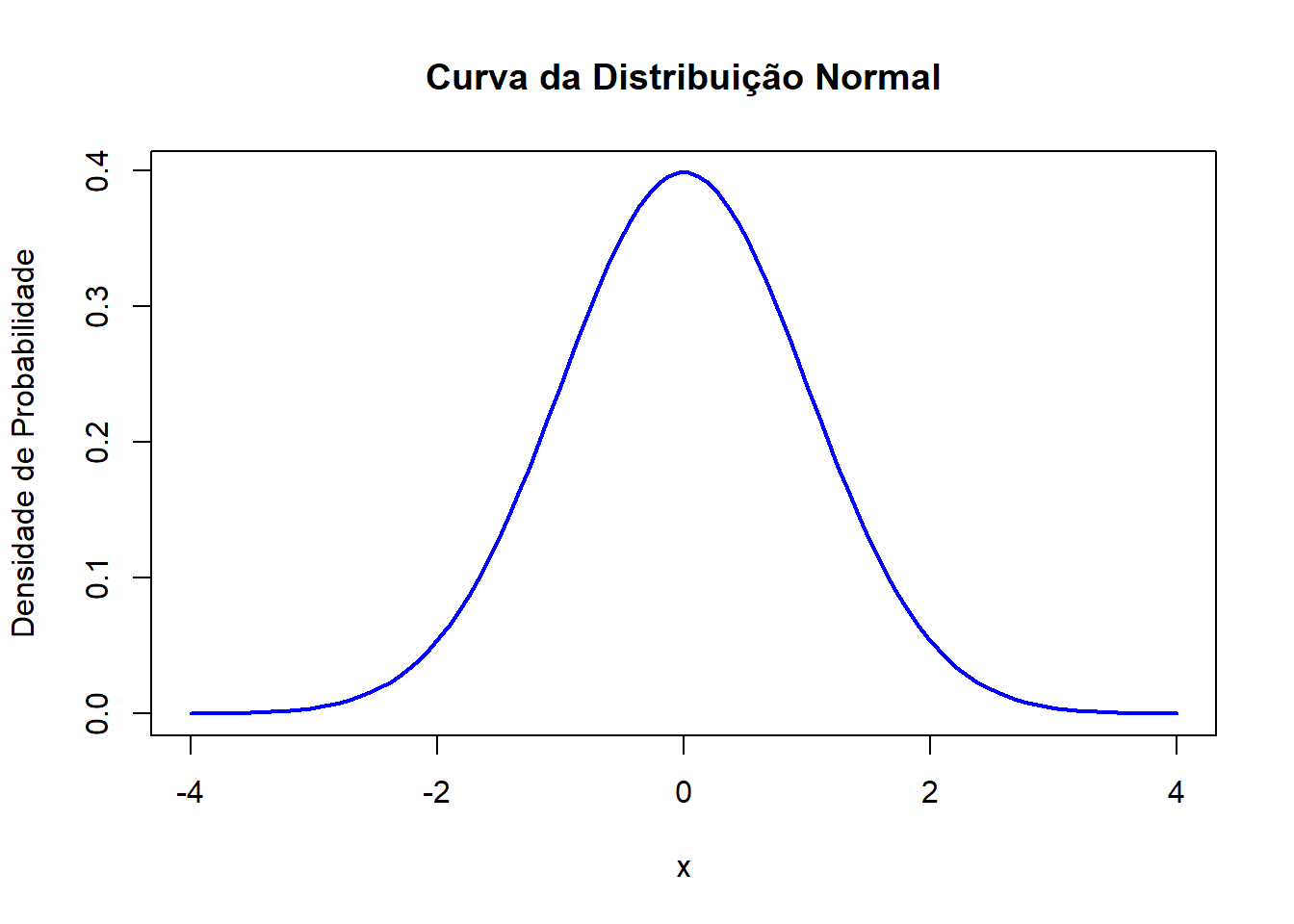

Atividade

  1. Pesquisar sobre as distribuições: exponencial e uniforme:

    • Elabore exemplos de uso dessas distribuições usando as funções em R apresentadas no exemplo da Normal

    • Calcule propbabilidades

    • Gere dessas distribuições para diferentes parâmetros

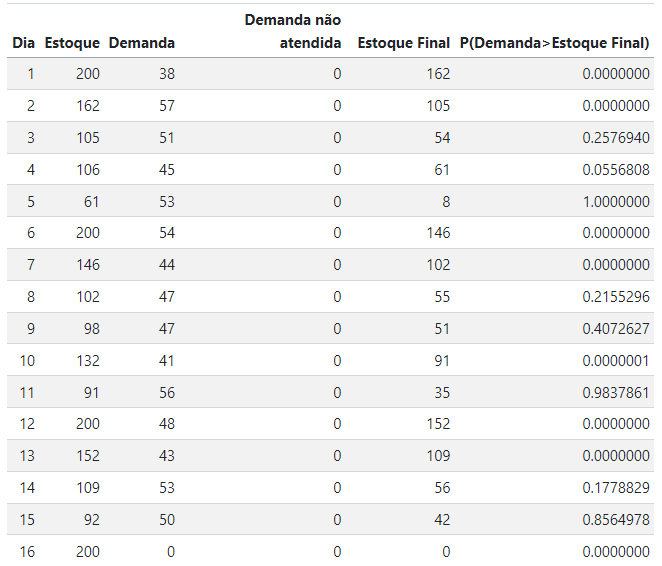
  2. A tabela abaixo mostra uma simulação de controle de estoque para 15 dias. Construa uma função para simular o controle de estoque. Considere:

    1. Estoque máximo: 200

    2. Estoque no dia 1 é o estoque máximo

    3. Demanda ∼\sim Poisson(50)(50)

    4. Sejam Prob=\mbox{Prob}= P(Demanda≥Estoque Final)P(\mbox{Demanda} \geq \mbox{Estoque Final}) e EDS=Prob×estoque máximo+estoque final dia anterior\mbox{EDS} = \mbox{Prob} \times \mbox{estoque máximo} + \mbox{estoque final dia anterior} o estoque do dia seguinte.

    5. O estoque do dia seguinte será preenchido considerando:

      1. Se Prob>0.10\mbox{Prob}>0.10 então o estoque do dia seguinte será o mínimo entre estoque máximo eEDS\mbox{EDS}, caso contrário o estoque do dia seguinte é o estoque final do dia anterior.
  • Dica: no dia 1, fixe o estoque máximo e simule a demanda usando rpois(n=1,lambda=50). Depois calcule a probabilidade de a demanda ser maior que o estoque final do dia 1 usando 1-ppois(Estoque final,50). Utilize a regra 5 para fazer os incrementos dos estoques diários

Referências